Present Value Table: A Complete Guide for Smarter Financial Decisions

After all, it is hard to relate $100,000 being spent today (a present value) to $300,000 that is expected to be received 20 years from today (a future value). By discounting that future $300,000 to a present value, we can more logically compare it to the $100,000 because both amounts will be expressed in present value amounts. If you received $100 today and deposited it into a savings account, it would grow over time to be worth more than $100.

• While useful, it is dependent on making good assumptions on future rates of return, assumptions that become especially tricky over longer time horizons.
• In many cases, investors will use a risk-free rate of return as the discount rate.
• You can also incorporate the potential effects of inflation into the present value formula by using what’s known as the real interest rate rather than the nominal interest rate.
• PV tables are great for quick estimates, but they’re locked to whatever interest rates and time periods are printed on the page.
• As you have seen, the frequency of compounding requires you to adjust the number of periods (n).

Present Value Tables Download

Present value calculations can be useful in investing and in strategic planning for businesses. It simplifies the process of calculating the present value of a single sum to be received in the future. There are many benefits to using a present value of Accounting for Technology Companies 1 table. Additionally, this table can help you make more informed financial decisions.

• The value of those future lease payments are discounted to the present value using a PV table (or a PV formula, but the table speeds things up).
• There are two interest payments per year for 10 years for a total of 20 payments.
• You’ll understand how much interest you’re actually paying, and how much of your payment is going toward principal.
• Present value, often called the discounted value, is a financial formula that calculates how much a given amount of money received on a future date is worth in today’s dollars.

Present Value Tables

As you can see from the present value equation, a few different variables need to be estimated. The cash flow from one period is simply the amount of money that is received on a future date. The rate of return is the estimated annual interest rate that will be received in the future. The number of present value of single sum table periods is simply the number of times the interest will compound over time. For example, if you are due to receive $1,000 five years from now—the future value (FV)—what is that worth to you today? Using the same 5% interest rate compounded annually, the answer is about $784.

PV of an Annuity

The present value of a single sum tells us how much an amount to be transacted in the future is worth today. For example, if you want to find the present value of $1 to be received in 5 years at an interest rate of 5%, you would find the intersection of the 5% interest rate row and the 5-year column. The resulting factor can be used to calculate the present value of a future sum. The discount rate in the PVIF table can then be multiplied by the cash amount to be received at a future date, and the result will be the present value of that sum. The present value formula is calculated by dividing the cash flow of one period by one plus the rate of return to the nth power. Some electronic financial calculators are now available for less than $35.

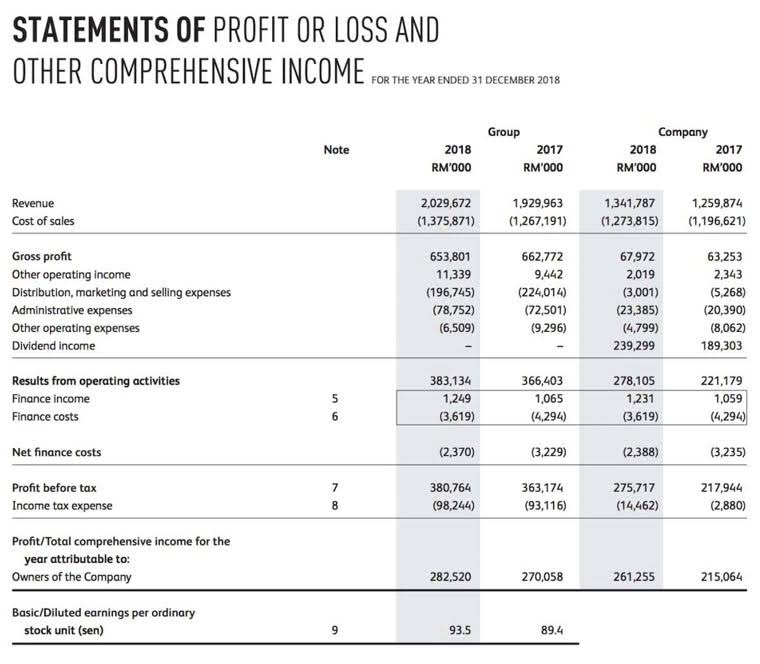
PV tables cannot provide the same level of accuracy as financial calculators or computer software because the factors used in the tables are rounded off to fewer decimal places. In addition, they usually contain a limited number of choices for interest rates and time periods. Despite this, present value tables remain popular in academic settings because they are easy to incorporate into a textbook. Because of their widespread use, we will use present value tables for solving our examples. Our focus will be on single amounts that are received or paid in the future. We’ll discuss PV calculations that solve for the present value, the implicit interest rate, and/or the length of time between the present and future amounts.

Likewise, the interest rate (i) must be adjusted to be compatible with (n). At the outset, it’s important for you to understand that PV calculations involve cash amounts—not accrual amounts. Add the two components together to calculate the present value of the bond. In the present value formula shown above, we’re assuming that you know the future value and are solving for present value.

• The interest rate is not stated, but the implicit rate can be determined by use of present value factors.
• Both investors and creditors use a present value calculator to evaluate potential investments and measure the return on current projects.
• Since the face rate is 8% and the market rate is 6%, these bonds will sell for more than face value or a premium.
• This is significantly less than the $160,000 in actual interest payments that will be made over the life of the bond, but remember that it has been discounted to the value of the investment today.
• Now we’ll look at what happens when interest is compounded (1) annually, (2) semiannually, (3) quarterly, and (4) monthly.
• These are often baked into the other tables but can be handy on their own for quick math.

Advance Your Accounting and Bookkeeping Career

If there are two or more future amounts occurring at different times for an investment, their present value can be determined by simply discounting each amount separately. For example, if an amount of $5,000 occurs at the end of two years, and a second amount of $6,000 occurs at the end of five years, you simply calculate the present value of each and combine them. Since the face rate of the bond is the same as the previous example, the interest payments are still $8,000 every six months.

• We see that the present value of receiving $1,000 in 20 years is the equivalent of receiving approximately $149.00 today, if the time value of money is 10% per year compounded annually.
• It is also important in choosing among potential investments, especially if they are expected to pay off at different times in the future.
• Let’s use a discount rate of 5% per annum for the calculation.
• Every investment, every loan, every retirement plan, every business forecast – they’re all bets placed on the value of tomorrow’s money.
• It sure would help if they know how much the $100,000 would grow if they invested it.
• Suppose that a company with an extra $100,000 lying around is trying to decide between investing the money at 4 percent for five years and using the extra money to expand the business.

A present value table is one of the most versatile resources in finance. You don’t need to be a finance nerd or an Excel wizard to use a present value table. Now, instead of using the PVIF formula directly, you can look up the factor in the Present Value of 1 Table. Advisory services provided by Carbon Collective Investment LLC (“Carbon Collective”), an SEC-registered investment adviser. Use the form below to generate your own present value of 1 table that can be printed or downloaded for use in Excel.

Determining the Discount Rate

Go a level deeper with us and investigate the potential impacts of climate change on investments like your retirement account. Double Entry Bookkeeping is here to provide you with free online information to help you learn and understand bookkeeping and introductory accounting. Chartered accountant Michael Brown is the founder and CEO of Double Entry Bookkeeping. He has worked as an accountant and consultant for more than 25 years and has built financial models for all types of industries. He has been the CFO or controller of both small and medium sized companies and has run small businesses of his own. He QuickBooks has been a manager and an auditor with Deloitte, a big 4 accountancy firm, and holds a degree from Loughborough University.